Simulation Speed in

Abstract

Moore's law

Along with density, the complexity of designs has increased, since it now requir es no more parts to make a design twice as complicated as it did two years ago. However, it is still more difficult to design and verify a design which has twic e the logic, and this fact has had an important effect on design methodology and the associated design tools. Indeed, the difficulty of designing more and more complex microprocessors was one of the reasons that RISC architectures were so a ttractive, since they were simpler to design, and the extra gates could be used for repetitive structures like registers and caches. However, we see that even w ith RISC architectures, the ability to put more and more logic on a single chip can not be ignored, and current RISC implementations are anything but simple, us ing millions of transistors.

Top-down methodology

Because design tools work with a representation, or model, of the design, the fo rm of that representation has had a central role in the design methodology. In a top-down methodol ogy, the representation is typically a hardware description l anguage (HDL). The HDL usu ally describes the design from initial concept to fin al layout. Figure 1 shows the steps in a top-down design methodology.

Fig. 1 Top Down Design Methodology

Increased simulation needs

When gate counts get to the hundreds of thousands, simulation needs become extre me. It is relatively easy to understand why this is the case by observing how th e new gates are used. When regular structures like memory elements are added to a design, the design complexity is not increased very much. See Figure 2.

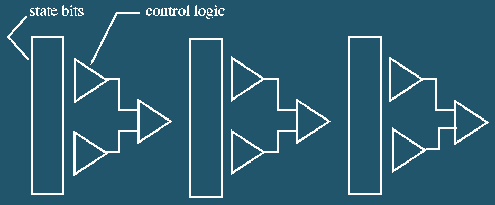
However, when random logic is added to a design, the new gates can be used for e ither more combinational logic or more bits of state. For example, a pipeline st age would add bits of state, while the controlling logic would be combinational. See Figure 3. When state bits are added, the design complexity goes up exponent ially, as each new bit of state increases the state space by a factor of two. Wh en combinational logic is added. the design complexity goes up at least quadrati cally, as each gate interacts with some percentage of the other gates. The numbe r of simulation test cases required to verify a design is more or less directly proportional to the size of the state space and the number of interconnections i n the combinational logic. Thus, the amount of simulation required increases exp onen tially with additional bits of state and quadratically with combinational l ogic gates.

C = a2 ^S + bR ² + cR + d

where

To put the problem in perspective, high-end workstations of the late 1980's were typically verified using test suites of a few million simulated CPU cycles. Wor kstations designed around 1990 were typically verified with 10's of millions of simulated cycles, and work stations of today are verified with 100's of millions . In every case, the designers would have simulated more if they had the resourc es.

Simulation Speed

Gate-level Simulation

Register-Transfer Level Simulation

wire sum3,sum2,sum1,sum0;

wire cout;

xor (sum0, a0, b0);

and (c0, a0, b0);

xor (sum1, a1, b1, c0);

and (t10, a1, b1), (t11, b1, c0), (t12, a1, c0);

or (c1, t10, t11, t12);

xor (sum2, a2, b2, c1);

and (t20, a2, b2), (t21, b2, c1), (t22, a2, c1);

or (c2, t20, t21, t22);

xor (sum3, a3, b3, c2);

and (t30, a3, b3), (t31, b3, c1), (t32, a3, c1);

or (cout, t30, t31, t32);

 Gate-Level Representation

reg [4:0] sum;

reg cout;

always @(a or b) begin

     sum = a + b;

     if (sum == 0) cout = 1;

     else cout = 0;

end

 RTL Representation

Fig. 4 Two Representations of a 4-bit Adder

Another opportunity to reduce the number of operations required can be found in parallel operations. For example, doing logical operations on buses is common in logic design, but in a gate level simulator, each gate involved would be execut ed separately. In a simulator at a higher level of abstraction, the operation wo uld be the logical operator applied to all the bits of the bus at once. This wil l often map on to a single instruction of the underlying host machine. See Figur e 5.

wire [7:0] out, in1, in2;

and (out[0],in1[0],in2[0]);

and (out[1],in1[1],in2[1]);

and (out[2],in1[2],in2[2 ]);

and (out[3],in1[3],in2[3]);

and (out[4],in1[4],in2[4]);

and (out[5],in1[5],i n2[5]);

and (out[6],in1[6],in2[6]);

and (out[7],in1[7],in2[7]);

 

Gate-Level Representation

wire [7:0] out, in1, in2;

assign out = in1 & in2;

 

RTL Representation

Fig. 5 Two Representations of an 8-bit And

There is another benefit from simulating at the same level as the design is done , and that is that the work of transforming the design into the lower level repr esentation can be avoided. In the design flow shown in Figure 1, the design done at Register-Transfer level should be verified at that level before doing the wo rk of logic synthesis. It can take a non trivial amount of time to synthesize a complicated design. That time is wasted if the design is incorrect and must be i terated through synthesis to make corrections.

Compilers vs. Interpreters

Once the designer is doing design verification at the pre-synthesis level, it is still impera tive for him to use the fastest simulator possible. Up until recen tly, nearly all simulators for hardware description languages were implemented a s interpreters. This was acceptable for gate-level simulation, but RTL and behav ioral level simulation is too slow when inter preted.

Consequently, new simulators are appearing which use compiled techniques. Compil ers for simulation languages are nothing new, of course, but the recognition tha t hardware description languages could be compiled just like general purpose sim ulation languages such as GPSS and Simula is relatively recent. While some compi lers translate to C first and then use the host machine's C compiler to complete the compilation process, and other compilers translate directly to machine code , the end result is that a machine language program is produced which implements the simulation model.

The performance result between the two techniques is dependant on the level of a bstrac tion. At gate level, interpretation is not all that inefficient, since ea ch gate evaluation can be performed by a table look-up, followed by propagation of each output result. However, as the evaluation operations get more complex, a s is the case with higher levels of abstrac tion, interpretation gets more and m ore expensive when compared to direct compilation. In the limit, the difference between an interpreted simulator and a compiled simulator is the same as the dif ference between an interpreter and a compiler for a general-purpose programming language. Typically, that difference is between one and two orders of mag nitude , with speed ratios of 40-50 being common.

Indeed, benchmark results between the VCS Verilog compiler from Chronologic Simu la tion and the interpreted Verilog-XL simulator from Cadence shows speed ratios from 1x at gate level to 40x at behavioral level. See Figure 6.
 

Model	Level	Execution Speed Ratio
bus model	Behavioral	40
microcontroller	Behavioral	31
video processor	RTL	27
pro cessor	RTL	14
pro cessor board	RTL	10
coprocessor chip	RTL	10
random logic netlis t	Gate	1

Fig. 6 Compiled vs. Interpreted Speed Ratios

Verilog vs. VHDL

An interesting question which is gaining increasing relevance, is are there any inherent properties of the HDLs themselves which affect simulation performance? If a designer can use either of two languages at the same level of abstraction, then the one which can simulate the fastest is the one which will let him get his job done soonest. Between the two major HDLs, Verilog and VHDL, the weight of evidence is that Verilog le nds itself to more efficient simulation than VHDL. Indeed, the VCS Verilog compi ler is far faster than any VHDL simulator on the market. Figure 7 has some recen t benchmark results compar ing several compiled VHDL simulators with VCS.
 

	Vantage	Cadence	Model Technology	Chronologic Simulation
Type of Output	C-code	native-code	Native-code	C-code
Language	VHDL	VHDL	VHDL	Verilog
execution time	278 sec.	212 sec	277 sec	53 sec

Fig. 7 Verilog vs. VHDL Simulation Speed

It has often been contended that VHDL provides a higher level of abstraction tha n Verilog does. One measure of the level of abstraction is the amount of work wh ich needs to be done to execute the model. That is, a simulation model must tran sition from one state to another in the same way as the real system being modele d (the abstract states and state transitions must be a homomorphic image of the real system's state space). If VHDL allowed a higher level of abstraction than V erilog, one would expect that the state space of the VHDL model would be smaller than the state space of the Verilog model. This, in fact, is not the case. At a ny given level of abstraction, the Verilog state space and the VHDL state space are more or less equivalent. Thus, simulators for the two languages must do the same number of state transitions. However, the increased generality of VHDL requ ires the simulator to do more work for each state transition. Consequently, we s ee Verilog simula tors faster than VHDL simulators.

Conclusion

As designs get more complex, simulation speed will become the overriding conside ration for selecting an HDL and simulator. Moore's law affects electronic design tools, as well as the electronics designs.