
The final HDI DFG implementation, integration and optimization efforts were accomplished during the Hardware/Software Detailed Design, Integration and Test development cycle. These development efforts had two critical aspects. The first was restructuring and modifying the HDI DFGs to fit in the Sharc 512 KByte on chip memory. The second challenge was reducing the HDI execution time to less than 1.5 seconds. These final development activities were accomplished in three phases. The first phase focused on capturing the full HDI DFG in GEDAE™ and replacing C code vector processing functions with optimized GEDAE™ function calls. The second phase was directed at streamlining the DFGs by eliminating unnecessary GEDAE™ family functions and replacing many of the complex DFGs, developed earlier, with more efficient C code primitives. The final phase concentrated on reducing the final memory utilization and optimizing the DFG runtime. In each these phases, modifications and/or improvements to the GEDAE™ tools or the Alex operating system software were needed to achieve the efficiency required the final HDI DFG design.
The following sections describe the initial HDI DFG primitive development efforts and final DFG implementation and optimization activities. For each cycle key development efforts are explained, the problems encountered are described, and the solution and results are discussed. The capture and optimization of the final HDI DFGs resulted in identifying number of shortcomings and improvements in the RASSP software development processes and tools. The following paragraphs are intended to provide insights for future developers on the lessons learned and tool capabilities required to capitalize on the benefits derived by applying the RASSP software development and autocoding process.
GEDAE™ was used to capture and autocode the SAIP HDI software for the distributed ALEX Sharc embedded processor architecture. GEDAE™ has a number of features that facilitate mapping complex signal processing application onto embedded COTS DSPs. While GEDAE™ provides significant capabilities for developing and optimizing embedded signal processing applications, at the time of the BM4 development effort it was still in beta test and a fully validated set of library functions did not exist. At the start GEDAE™ had a fairly complete set of basic library functions for single precision floating point. However, the library was very sparse in functions for other data types. In addition, the existing library had not been thoroughly tested. In the process of implementing the initial HDI algorithms, errors were found and corrected in 13 of the existing GEDAE™ library functions. While using GEDAE™ to implement the HDI DFG ultimately provided a highly efficient software implementation, tool and library immaturity issues did result in lower than anticipated productivity.
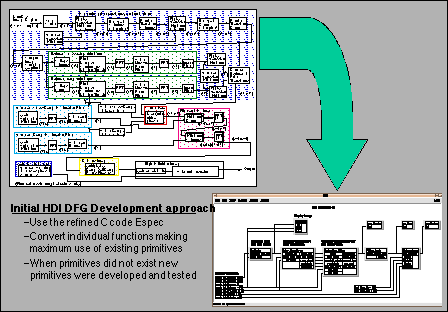
The initial part of the HDI algorithm, the "Remove Prior Transforms" algorithm, was straight forward as far as conversion to a data flow paradigm. The initial design approach was to use existing library primitives whenever possible. There are advantages to using existing GEDAE library primitives that have been optimized and tested. The first advantage is that the DFGs can be easily captured using these primitives and the DFG development time can be reduced. The second is that GEDAE™ provides the capability to directly distribute the functions onto embedded COTS DSP boards without any modifications of the functions or flow graphs. In order to capitalize on these advantages, the initial HDI DFG development effort emphasized the use of existing primitive functions.
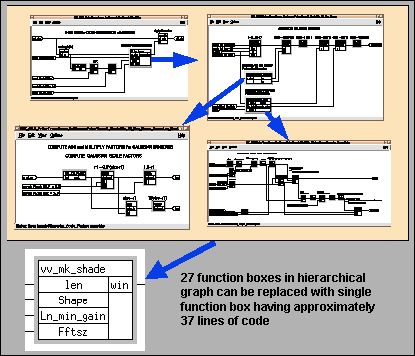
In the case of the HDI DFG many of the preprocessing functions required complicated indexing, sampling and mathematical functions specific to the HDI algorithm and as a result did not exist as GEDAE™s library functions. As a result, these unique functions were captured as DFGs using very low level GEDAE library primitives (e.g. add, subtract, multiply, etc.). This approach led to highly complicated DFGs with multiple levels of hierarchy that were difficult to follow and understand. These complicated DFGs later created in large GEDAE™ execution schedules and increased program memory requirements. To resolve these problem, many of these HDI DFGs were replaced by higher level HDI specific C code primitives which were not only complicated but significantly more efficient. Figure 2 shows an example of the difference between a low level DFG versus a custom C code primitive.
Developing a GEDAE™ primitive requires definition of the input and output data types and identifying the appropriate embeddable library function or functions, to take advantage of optimized calls for a given processor. GEDAE™ requires separate primitives for each input/output data type (i.e. integer, float or complex). In order to take advantage of the optimized vector operations on certain DSPs, separate functions are also needed for the different input and/or output data arrays (i.e. stream data, vector data, matrix data, variable length vector data or variable size matrix data). Primitive functions may be as simple as adding two inputs and outputting the result, or multiplying the input by a constant. Simple primitives can include trigonometric, transcendental, type conversion, or logical compare functions. Other primitives may be more complex such as FFT, matrix inversion or file I/O functions. A function box may be as complex as the developer cares to make it. In some cases an entire algorithm may be encapsulated as a GEDAE™ primitive.
Some of the HDI primitives required variable length inputs and/or outputs. At the start of the HDI DFG development effort, GEDAE™ did not support variable length vectors or matrices. As a result, primitives were created using the maximum fixed data size with separate data parameters specifying the variable sized data sets. This added extra data paths in the flow graph and increased memory requirements. Later when GEDAE™ upgraded to incorporate the ability to handle variable length data sets, these functions were rewritten creating additional productivity losses. Although the flow graphs were simplified with the introduction of variable length data types, no memory savings were realized because the variable length data arrays were still statistically allocated up for their maximum size.
During the early HDI DFG implementation efforts, a number of problems were found. Among these were problems with the way GEDAE™ creates and handles input/output data queues. In one case, queues were created for parallel data paths that caused wait conditions that deadlocked the DFG execution. Another time GEDAE™ inserted queues where they were not necessary and reported graph errors. Variable length vector and matrix operations caused problems when the function was performed in place. There was also a problem with variable length data when the amount of output data was not the same as the input. This problem was resolved by incorporating "produce" commands for the variable size length data as well as on the data itself. Another problem encountered was difficulty in identifying and correcting DFG errors. When a DFG failed during the reset method, GEDAE™ reported the error as occurring in a group, where a group was all of the consecutive function boxes running on a single processor. This made pinpointing the error difficult. We were only able to find the error by adding a file output box to a flow graph and analyzing the resulting data. Various support functions were written to aid in debugging and in testing the results. These included functions to write various data types to a file for comparison with the baseline HDI algorithm as well as function boxes to display them as images. On the positive side GEDAE™ provided tools allowing the user to manually break the graph into arbitrary groups for locating errors.
As individual problems were identified, they were passed onto the GEDAE™ development team. During the course of the initial as well as the final HDI DFG development effort, most of the problems were corrected or alternative implementations were identified. As a result the BM4 DFG development effort a number of key improvements and extensions were made to GEDAE™. In addition, the GEDAE™ function library has been extended and tested and now includes most of the primitives required for HDI DFG.
In the course of developing the initial HDI DFGs and primitives, a key lesson learned was that for complex flow graphs, a top down DFG design approach is crucial. Understanding the algorithm is essential to efficient DFG implementation. MIT/LL's HDI executable specification code, much of which had been translated from MATLAB, provided an accurate computational specification of the HDI algorithm. However, in many instances, MATLAB's use of computed array indexing and other coding constructs obscured the computational functions, made them difficult to understand, and did not provide a good implementation specification. As a result, literal translation of the executable specification C code into GEDAE™ primitives and DFGs was not an efficient approach for capturing the HDI algorithm. Once we realized this, many of the early, highly complex DFG's and primitives were rewritten as simplified, HDI specific C code functions and encapsulated as application specific primitives.
At the end of the initial HDI DFG development effort, all of the primitives and DFGs for the "Remove Prior Transforms" portion of the HDI algorithm had been captured and tested. In some instances these initial DFGs were complicated and difficult to understand but functionally correct. We had also identified a number of DFG elements that could be optimized to reduce the DFG complexity, execution times and memory usage.
Based on these results, the HDI final DFG optimization efforts were focused on two critical aspects. The first was restructuring and modifying the HDI DFGs to reduce the on chip memory requirements. The second challenge was reducing the HDI DFG execution time to less than 1.5 seconds. An iterative, three cycle process was used to attack these issues. Each of the optimization cycles focused on analyzing memory use and execution times, and implementing DFG improvements to reduce the memory use and execution times. The following tables show the memory use and the execution time at the end of each of the optimization cycles. In the following paragraphs the changes made to achieve those improvements and lessons learned during each of the phases are described in more detail. During each cycle the problem was attacked from two aspects. First, changes were made in the HDI DFG implementations. Second, improvements were identified and made in the GEDAE™ and Alex software tools to enhance the memory and execution efficiency.
| Cycle 1 * | Cycle 2 ** | Cycle 3 | |
| Static Data (GEDAE™ Function Box Locals) | 19,000 | 19,000 | 14,004 |
| Route Table | 20,000 | 20,000 | 8,471 |
| Program Memory | 55,000 | 48,000 | 40,488 |
| Schedule Memory | 100,000 | 70,000 | 37,062 |
| GEDAE™ Schedule and Admin | 9,000 | 9,000 | 2,466 |
| Function Box State | 1,281 | 1,281 | 1,281 |
| Send/Receive Data Buffers | 2,048 | 2,048 | 1,376 |
| Other overhead | 12,000 | 12,000 | 8,912 |
| Total | 218,329 | 181,329 | 114,060 |
| All sizes are in words * These are estimates based on known savings. ** These are a combination of measured and estimated. | |||
| Execution Times for the HDI Algorithm | ||||||
| Cycle 1 | Cycle 2 | Cycle 3 | ||||
| Single | Total | Single | Total | Single | Total | |
| Remove Prior Transforms | 0.41399 | 0.36370 | 0.07086 | |||
| MRFFT (79 FFTs by 96 pnts) | 0.14087 | 0.12563 | 0.02244 | |||
| MRFFT (96 FFTs by 96 pnts) | 0.17034 | 0.15292 | 0.02714 | |||
| Center | 0.04335 | 0.03213 | 0.02342 | |||
| Filter and Decimate Range | 0.33545 | 0.22848 | 0.13248 | |||
| Filter and Decimate X Range | 0.37369 | 0.25265 | 0.14072 | |||
| FFT (12 FFTs by 16 pnt) x 180 | 0.00007 | 0.14688à | 0.00077 | 0.13914 | 0.00023 | 0.040550 |
| Focus | 0.10039 | 0.03403 | 0.01026 | |||
| HDI | 2.06090 | 1.04154 | ||||
| Generate Kernels | 0.01035 | 0.00127 | ||||
| Make Looks x 64 | 0.00247 | 0.15827 | 0.00071 | 0.04518 | 0.00048 | 0.03098 |
| MGS x 64 | 0.00639 | 0.40915 | 0.00461 | 0.29491 | 0.00249 | 0.15942 |
| Back Solve x 64 | 0.00122 | 0.07782 | 0.00082 | 0.05229 | 0.00062 | 0.03977 |
| Decompose summed | 0.02794 | 1.23228 | 0.01275 | 0.71143 | 0.00686 | 0.37844 |
| Transpose summed | 0.00074 | 0.03057 | 0.00059 | 0.02423 | ||
| Weighted Norm summed | 0.01717 | 0.22759 | 0.01525 | 0.17395 | 0.00568 | 0.23196 |
| MLM summed | 0.00240 | 0.700827 | 0.00114 | 0.66256 | 0.00110 | 0.10131 |
| Dot Product summed | 0.00087 | 0.03560 | 0.00111 | 0.04684 | 0.00110 | 0.04490 |
| Logarithm summed | 0.00055 | 0.02049 | 0.00062 | 0.02556 | 0.000054 | 0.02197 |
| Total with event collection | 4.25375 | 2.970627 | 1.41896 | |||
| Total without event collection | 1.38278 | |||||
| Numbers in "Single" columns are measured. Numbers in "Totals" columns are a sum of individual firings. 3 firings are much larger because of iteration. FFTs performed individually so x 2160. | ||||||
The initial optimization cycle focused on restructuring the functionality of the DFG. Code that was easily recognized as known signal processing primitives such as vector multiplies and dot products were replaced with GEDAE™ library functions. Portions of code that were not fundamental signal processing operations were left as encapsulated C-code custom primitives but obvious vector operations were replaced with optimized vector library functions. The focus, decompose, and MLM parts of the algorithm were encapsulated. Only small amounts of the decompose and MLM code were replaced with vector operations. The indexing scheme used in decompose to take advantage of the kernel symmetries resulted in code that was difficult to implement with vector/matrix operations. As it turns out, decompose and MLM accounted for almost half of the algorithm execution time. Also, GEDAE™ 's current implementation of families, while efficient if distributed, makes relatively in-efficient use of memory and CPU when executed on a single CPU. As a result, most of the family functions were removed during first phase. Finally, the decompose function, which operates on 64 sub-regions, was sub-scheduled to reduce memory use.
One opportunity to improve memory efficiency was the use of sub-schedules. "For loops" are generally used to process multiple data items that are processed identically. For example, if it is necessary to low pass filter (lpf) each row of a matrix, we would loop over the rows and apply the lpf to each row. In GEDAE™ there are two ways that can be done. First, you can demux the array into a family of vectors and apply the operation to each vector simultaneously. Conceptually this is a spatial separation that allows the developer to process each vector on a different processor as a family function. This provides an effective approach for distributing repetitive functions across multiple processors. However, currently there is a significant overhead associated with the family approach. Each family member is allocated as a separate instance of the function box, with its own data memory allocation. Nothing can be done to reduce this overhead. The second method to do this is to convert the matrix into a single stream of vectors (each row becomes a vector) and to process them sequentially (time multiplexing). This forces the processing to be done on a single processor. The time multiplexing approach creates only one instance of the function box, but will allocate the memory required to process all the vectors simultaneously (see figure 3). Fortunately, GEDAE™ provides the ability to sub-schedule the vector processing. The sub-schedule basically sends one vector at a time through the vector processing box. This significantly reduces the memory requirements (see figure 4).

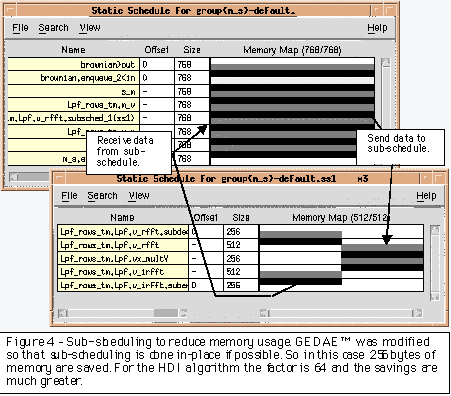
It is important to realize this was not an algorithmic break through. The natural way to process the HDI 64 image chip sub-regions was to use a for-loop. In this case, memory only needed to be allocated for one sub-region at a time. In any case, the initial implementation made extensive use of family syntax and during the first cycle most of the family notation was removed to reduce memory use.
A second change made during phase one was to use vector routines wherever possible. Obvious dot products or vector operations were replaced by calls to the GEDAE™ optimized library. This significantly improved the execution time (from more than 10 seconds to just over 4 seconds). However, there were still large portions of the algorithm that were C code and could be improved.
The result of the phase one improvements was a graph that functioned correctly but would still not fit in the Sharc internal memory. The execution time was greater than 4.0 seconds. While we expected some improvement by using the Wideband optimized library functions, we didn't expect a factor of 2 improvement. Still we had a sound implementation that was the basis for additional optimizations
While at the end of the first cycle both performance and memory efficiency were improved, they had to be reduced further if we were to meet the objectives of the program. It was obvious that execution times of less than 2.0 seconds were not going to be realized without significant changes to the implementation. A decision was made to modify the DFG functional implementation to improve both memory and computational efficiency.
Phase 2 focused on completely removing the use of families and restructuring the DFG so the majority of the custom code could be replaced with optimized vector operations. The first step was to analyze the code and determine which of the custom C code routines could be replaced with small amounts of C code combined with course granularity vector operations. There were a number of things that contributed to making the HDI code difficult to implement with vector operations. The index arrays used to take advantage of some of the kernel symmetries made using vector operations difficult. The problem was that the symmetry was applied inside a for-loop. The indexing was removed and replaced with operations that applied the symmetry at a vector level. Further analysis and simplification of the code revealed that the underlying operations in the decompose function were matrix multiplies. Further, the "looks" were non-rectangular because the corners were removed. By simultaneously fixing all these problems it was possible to implement most of decompose with matrix multiplies, adds and subtracts. In the process we were able to further reduce the size of the kernels and save a significant amount of memory.
A key reason for the slow progress in optimizing the DFG was the parallel implementation of GEDAE™ enhancements. Two issues contributed to the slow down. First, progress couldn't be made until the enhancements were available. Second, progress was hampered by the discovery of bugs associated with the enhancements. We also encountered a series of problems associated with the ADI compiler. These problems were particularly difficult to uncover because of the limited debugging capabilities provided by Alex and Analog Devices. An Ixthos Sharc board was used to debug parts of the code because it provided a better I/O library and debugging tools.
During the second phase families were completely removed from the implementation and the encapsulated code for focus, make-looks, decompose and MLM was re-coded to use optimized signal processing functions. Additionally, decompose, generation of vectors, and make-looks were simplified by setting the corners of the looks to 0.0 rather than removing them from the data structure. Decompose was the only routine that was hard to simplify. It wasn't until the code had been re-worked that it became obvious that decompose could be implemented with matrix multiplies. The approach taken was to:
At the end of the second phase the goal of less than 2.0 seconds was clearly in reach. The execution time was just under 3.0 seconds but benchmarks and analysis indicated that a reduction to 2.0 seconds or less was likely. The most difficult problem that remained was the challenge of fitting the DFG into the Sharc on chip memory. The analysis of the problem indicated that achieving the memory requirement was possible.
It was evident at the end of the second cycle that we had some difficult problems to deal with. It appeared that achieving the performance goal was likely but achieving the memory goal (fitting it in the on-chip memory of a single Sharc) was questionable. The amount of memory used by GEDAE™, combined with the HDI code size and the large data sets made fitting the DFG on a single processor very difficult. This final phase considered every opportunity to reduce memory use. Some savings required enhancing GEDAE™. Others required modifying the HDI implementation. The final phase also included integrating the optimized Wideband library functions that take advantage of operands distributed between SRAM 0 and SRAM 1.
The final phase involved only a few changes in the algorithm implementation. It primarily depended on changes to GEDAE™ that would enable additional optimizations. It was clear GEDAE™ was using more memory than necessary. There were some obvious optimizations that could afford significant reductions in memory use. The GEDAE™ developers implemented these enhancements and a several changes were made to the DFG to take advantage of them. As a byproduct of the changes, GEDAE™ was upgraded to provide the user with the capability to analyze and control memory use. As a result, it was relatively simple to juggle memory and fit HDI into a single Sharc processor. The two most important changes made in the DFG were:
There were three other GEDAE™ enhancements that improved its memory efficiency.
GEDAE™ was also enhanced to execute static schedules more efficiently. The biggest savings came from removing the overhead for collecting trace events when the trace buffer size was set to 0. The total savings in this case were approximately 50 msecs. The Alex port was also changed to use less memory for routing data. This resulted in a saving of about 52 kbytes. A number of additional changes were made to the DFG in the final phase to take advantage of the GEDAE™ enhancements and to make use of the more efficient optimized algorithms available.
In summary, the final optimizations of the HDI DFG were focused on reducing memory use. The GEDAE™ and the Alex operating system enhancements were used to implement changes to the DFG, to reduce the on chip memory requirements. Changes were made to GEDAE™ to allow functions to be executed in place, eliminating the need for two copies of the large HDI data arrays. GEDAE™ was updated to move the memory allocation function off the embedded processor. Finally, changes were implemented to allow memory to be reused by static sub-schedule functions instead of allocating memory for each subschedule. These three changes resulted in combined savings of more than 112 Kbytes of the on chip memory. In addition, the Alex embedded processor port software was modified to reduce the communications routing table by 60% (from 80 Kbytes to 34 Kbytes). The remaining memory reductions were accomplished by changing the HDI DFG using GEDAE™'s enhanced capabilities for displaying and modifying the Sharc SRAM memory map. Overall memory usage was decreased from 724 Kbytes to 456 Kbytes which could be accommodated in the Sharc on chip SRAM.
Once the embedded real-time code fit in the on chip memory, final runtime optimizations could be accomplished. With the incorporation of the Wideband optimized dual fetch library functions and several other minor changes, the HDI DFG execution time was reduced to 1.42 seconds.
Optimizing the HDI DFG to fit in the on chip SRAM and achieving an execution time of less than 1.5 were significant challenges. The optimization efforts were hampered by a need for a number of improvements and extensions to the GEDAE™ and Alex software. Identifying problems areas and coordinating GEDAE™ and Alex software enhancement efforts proved to be time consuming and costly. However, in the end, the software tools provided the enhanced memory management and execution control capabilities needed to achieve realtime embedded system requirements.
In retrospect, having a better defined, efficient DFG development process would have significantly increased the efficiency for the BM4 DFG development effort. Because of the limited number of applications that had been implemented in GEDAE™, at the start of the BM4 development effort we did not have a proven, well defined process. In addition, previous DFG development efforts had not dealt with an application as complex as HDI or attempted to achieve the memory utilization or runtime efficiency required to achieve BM4 objectives. As a result, during the course of BM4 a number of lessons were learned and a number of improvements were made to the autocoding tools and processes.
Some of the key lessons learned, which will improve the process for future DFG developments, are:
In accomplishing the BM4 HDI DFG development effort a number of key extensions were made to GEDAE, which enable more efficient memory utilization and execution. These included; the ability to manage and control the internal memory resources, the ability to schedule and subschedule functions in place reduce memory allocation, significant improvements in the scheduler which reduced both memory requirements and execution time, as well as primitives library corrections and extensions. All of these changes and extensions, as well as future improvements will continue to enhance GEDAE™'s capabilities and benefits for developing and implementing signal processing applications.
GEDAE Primitives Developed to Support HDI Software Development
The HDI primitive functions were named based on the functionality of the box as well as the data type of the data being processed. This naming convention was beneficial in locating the desired function as well as understanding a flow graph that uses the function. Functions of the same type and mode were stored in separate directories for ease in locating the desired function. The following prefix conventions were used to identify data type and mode of the function boxes.
| Prefix | Data Type | Data Mode |
| none or s_ | Float | Stream |
| v_ | Float | Vector |
| m_ | Float | Matrix |
| vv_ | Float | Variable Length Vector |
| vm_ | Float | Variable Size Matrix |
| x_ | Complex Float | Stream |
| vx_ | Complex Float | Vector |
| mx_ | Complex Float | Matrix |
| vvx_ | Complex Float | Variable Length Vector |
| vvmx_ | Complex Float | Variable Size Matrix |
| i_ | Integer | Stream |
| vi_ | Integer | Vector |
| mi_ | Integer | Matrix |
| vvi_ | Integer | Variable Length Vector |
| vxi_ | Integer Complex | Vector |
| vmi_ | Integer | Matrix |
In addition the letter K is used to indicate that input parameters were constant rather than variable. A convention was also adopted to differentiate the hierarchical DFG function names. Top level flow graph functions were identified using all capital letters, intermediate function names were capitalized, and primitive functions were given lowercase names. GEDAE™ indicates that a box is hierarchical by graphically highlighting the function boxes, however this may not be shown on a hardcopy of the DFG or from the flow graph filenames.
The following 126 GEDAE™ primitive functions were develop as part of the initial HDI DFG algorithm software development effort. Those functions preceded by '**' indicate the 17 boxes that were considered to be HDI specific. Another 14 which are preceded '*' were identified as being reusable but probably would not be included in a standard library of functions. The remaining 95 primitive functions, while unavailable at the time of the BM4 development, are expected to be included in the final GEDAE™ function library.
| Box Name | Box Function |
| **C_decompose_mgs | C_decompose with index for Modified Gramm-Schmidt |
| Kif_else | Set output to input constant or to input value depending on input flag being true or false |
| V_constant | Create constant vector |
| V_printf | Print constant vector to file |
| **cdone_i | Convert candiateDone data to int stream for candidateDone flat file |
| **decompose_mgs | Decompose for Modified Gramm-Schmidt using 2-D decompr array |
| dvx_mrfft | Computes complex FFT or inverse FFT of size N |
| eqK | Set output = true if input == constant, = false ow |
| geK | Set output = true if input >= constant, = false ow |
| gtK | Set output = true if input > constant, = false ow |
| **hdi_fprintf | Print one float/line to file using specified format (float stream input) |
| **hdi_vfprintf | Print one float/line to file using specified format (vector input) |
| **hdi_vxfprintf | Print one complex # /line to file using specified format (complex vector input) |
| **hdi_xfprintf | Print one complex # /line to file using specified format (complex stream input) |
| **i_candStart | Convert int stream from candidateStart flat file to data values for candidateStart |
| **I_constant | Set integer output stream to constant integer value |
| i_mi | Convert int stream to int matrix of constant size C x R |
| i_mx | Convert complex integer stream to complex integer matrix of size C x R |
| *i_mx_flat | Convert int stream to complex matrix. i[0] = R, i[1] = C, i[2] = datatype, i[[3]-i[3+R*C*2] = complex |
| *i_next_pow2 | Find next higher integral power of 2 greater than input integer |
| i_vi | Convert intr stream to integer vector of constant size C |
| *i_vmx_flat | Convert int stream to var complex matrix. i[0] = R, i[1] = C, i[2] = datatype, i[[3]-i[3+R*C*2] = complex |
| if_else | Set output = input1 or input2 depending on input flag being true of false |
| if_elseK | Set output = input or to constant depending on input flag being true or false |
| leK | Set output = true if input <= constant, = false ow |
| ltK | Set output = true if input < constant, = false ow |
| **m_mgs | Modified Gram-Schmidt. Assumes # rows < # cols |
| m_s | Convert matrix to stream |
| m_selsub | Select sub matrix from matrix |
| **mgs | Modified Gramm Schmidt (fixed size) |
| mi_i | Convert int matrix to int stream |
| **mlm_confm2 | mlm_confm for mgs with 2D decompr array |
| **mx_Focus | Multiply by range and Xrange focus phasors |
| *mx_PartSubMxN | Select part of complex matrix |
| mx_disp | Convert Complex Matrix to Real for Display |
| *mx_mmultsubarea | Multiply real matrix times subarea of complex matrix |
| mx_rotate | Rotate a complex matrix 180 degrees |
| mx_selsub | Select subarea of complex matrix |
| mx_selsubd | Select subarea of complex matrix (Dynamic output) |
| mx_selsubvmx | Select subarea of complex matrix (var matrix output) |
| *mx_vmxinsrt | Insert variable length complex matrix into complex |
| matrix neK | Set output = true if input != constant, = false ow |
| **printcandStart | Print selected values from candidate start message |
| s_m | Convert stream to matrix of constant size |
| *s_mx_flat | Convert stream to complex matrix. s[0] = R, s[1] = C, s[2] = datatype, s[[3]-s[3+R*C*2] = complex |
| s_v | Convert stream to vector of constant size |
| *s_vmx_flat | Convert stream to var complex matrix. s[0] = R, s[1] = C, s[2] = datatype, s[[3]-s[3+R*C*2] = complex |
| select | Set output = input1 or input2 based on flag (both inputs are consumed) |
| selectK | Set output = input1 or constant based on flag (input is consumed) |
| selectKK | Set output = constant1 or constant2 based on flag (input is consumed) |
| v_KaKm | Add constant scalar to vector and multiply by constant scalar out[i] = (in[i] + A) * M |
| *v_cbthrK | Select the longest continuous block of values in vector above constant threshold K. |
| *v_cntthr | Select the longest continuous block of values in vector above constant threshold K and its length |
| **v_dct3 | Compute the first three terms of the Discrete Cosine Transform. |
| v_mults | Multiply vector times a stream scalar out[i] = in[i] * s |
| v_power_a2b | Raise vector to power of second vector out[i] = in1[i] ** in2[i] |
| v_s | Convert vector to stream |
| v_smult | Multiply vector by a stream scalar out[i] = in[i] * s |
| v_sramp | Create a vector = linear ramp from constant start S0 with constant increment Inc for n samples. |
| vi_i | Convert integer vector to integer stream |
| **vm_mgs | Modified Gram-Schmidt. Assumes # rows <= # cols (variable matrix input) |
| vm_mtran | Matrix Transpose of variable length matrix |
| vm_mult | Matrix Multiply of variable matrices |
| vm_size | Returns size of variable matrix |
| vm_s | Convert variable matrix to stream |
| *vmx_mxinsrt | Insert variable length complex matrix into complex matrix |
| vmx_rotate | Rotate a complex variable matrix 180 degrees |
| vmx_size | Returns size (# columns and # rows) of variable complex matrix |
| vmx_trans | Transpose variable length complex matrix |
| vmx_vmmult | Point by point multiply of variable complex real matrices |
| *vmx_vmxinsrt | Insert one variable length complex matrix into another |
| vmx_x | Convert variable complex matrix to complex stream |
| vv_KaKm | Add constant to variable vector and multiply by constant out[i] = (in[i] + A) * M |
| vv_abs | Absolute Value of variable vector out[i] = abs(out[i]) |
| vv_add | Add two variable vectors out[i] = in1[i] + in2[i] |
| vv_addK | Add constant to variable vector out[i] = in[i] + K |
| vv_adds | Add stream scalar to variable vector out[i] = in[i] + s |
| **vv_cbthrK | Select the longest continuous block of values in var vector above constant threshold K. |
| vv_concat | Concatenates two variable length vectors out[i] = in1[i] out[j+N1] = in2[j] N1 = len (in1) |
| vv_cos | Cosine of variable vector out[i] = cos(in[i]) |
| vv_dim | Returns (maximum) dimension of variable vector as a stream |
| vv_dimK | Returns (maximum) dimension of variable vector as a constant |
| vv_exp | Exponential of variable vector out[i] = exp(in[i]) |
| vv_fprintf | Print to file one value/line of variable vector with specified format |
| *vv_insert | Insert variable vector into second variable vector at constant location |
| *vv_inserts | Insert variable vector into second variable vector at variable location |
| vv_mult | Multiply two variable vectors |
| vv_multK | Multiply variable vector by constant |
| vv_mults | Multiply variable vector by stream scalar |
| vv_padd_vm | Form variable matrix from 2 variable vectors c[i][j] = a[i] + b[j] i = 0,nǃ and j = 0,mǃ |
| vv_pow_in2K | Variable vector to constant power |
| vv_pows | Variable vector to stream scalar power |
| vv_s | Convert variable vector to stream |
| vv_sasm | Add stream scalar to variable vector and multiply by stream scalar out[i] = (in[1] + a) * m |
| vv_sdiv | Divide stream scalar by variable vector out[i] = s/in[i] |
| vv_selem | Sum of elements of variable vector |
| vv_selsubs | Select variable subvector of length N from variable vector starting at element L |
| vv_size | Returns length of variable vector |
| vv_smult | Multiply variable vector by stream scalar |
| vv_sramp | Create a variable vector = linear ramp from S0 with increment Inc for n samples. |
| vv_subs | Scalar subtraction of variable vector and stream scalar out[i] = in[i] - s |
| vv_v | Convert variable vector to vector |
| vv_vm | Convert r variable vectors to variable matrix where r is stream scalar |
| vv_vm1Dcol | Convert variable vector of size k to variable matrix of size 1 x k (cols x rows) |
| vv_vm1Drow | Convert variable vector of size k to variable matrix of size k x 1 (cols x rows) |
| vv_vmK | Convert R variable vectors to variable matrix where R is constant |
| vv_vz | Convert variable vector of size n, max size MAX to vector of size MAX with zero fill |
| vvx_cmplx | Combine two real vectors into single complex vector |
| vvx_constant | Create variable complex vector with constant value |
| vvx_fft | FFT for variable complex vectors |
| vvx_ifft | inverse FFT for variable complex vectors |
| vvx_rmult | Multiply variable complex vector by variable real vector |
| vvx_rot | Rotate variable complex vector 180 degrees |
| vvx_split | Split variable complex vector into variable real and imaginary vectors |
| vvx_vmx | Convert variable vectors to variable matrix |
| vvx_vx | Convert variable complex vector to complex vector |
| vx_0fill | Fill end of complex vector with zeros |
| vx_mrfft | Computes complex FFT or inverse FFT of size N |
| vx_shift | Shift complex vector |
| vx_vvx | Convert complex vector to variable complex vector |
| vx_zpad | Fill end of complex vector with zeros |
| x_mx | Convert complex stream to complex matrix of constant size |
| x_read_file | Reads complex data matrix of size rows x cols from a file |
| x_reread2 | Reads 2 complex data matrices from 2 files and outputs them alternately |
| x_reread_2 | Reads 2 complex data matrices from 1 file and outputs them alternately |
| x_vmx | Convert complex stream to variable complex matrix |