The next class of synthesis tools deals with layout external to the cell. Since most active circuitry is inside the cells, these tools handle the tasks of intercell wiring (routing), cell placement, and pad layout. Since routing can be very complex and can consume more area than the actual cells do, it is important to plan the connections in advance. Although proper cell planning and placement can make the routing simpler, tools that do this automatically are rare.
A router is given sets of points on unconnected cells that must be connected. The space between these cells can be as simple as a rectangle or as complex as a maze (see Fig. 4.7). When the routing space is rectangular and contains connection points on two facing sides, it is called a channel. When routing is done on four sides of a rectangular area, it is called a switchbox. More complex routing areas usually must be decomposed into channels and switchboxes. Many different techniques exist for routing, depending on the number of wires to run, the complexity of the routing space, and the number of layers available for crossing.
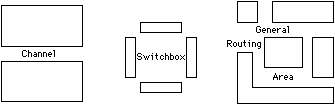 |
| FIGURE 4.7 Routing areas. |
Maze routing is the simplest way to run wires because it considers only one wire at a time. Given the connection points and a set of obstacles, the maze router finds a path. The obstacles may be cells, contacts that cannot be crossed, or wires that have already been run.
| The first maze-routing technique was based on a grid of points to be traversed by the wire [Moore; Lee]. Now known as the Lee-Moore algorithm, it works by growing concentric rings of monotonically increasing values around the starting point. When a ring hits the endpoint, a path is defined by counting downward through the rings (see Fig. 4.8). This method is so simple that hardware implementations have been built [Blank]. It can also employ weighting factors that increment by more than one and use the lowest value when two paths merge. This can prevent wires from running outside of an area when they could run inside. |
|
One problem with Lee-Moore routing is that it demands a work array that is very large. Moore observed that the integers 0, 1, and 2 can be used cyclically since the adjacent values are always plus or minus one. However, even a two-bit work array can be very large. To avoid this problem, maze routing can be done with traditional maze-solving techniques that walk along the obstacle walls. Figure 4.9 illustrates this technique: The router moves from the starting point toward the finish until it hits an obstacle. It then chooses to walk to the left (although it could choose to walk to the right, so long as it is consistent). When the obstacle is cleared, it heads for the endpoint--but once again hits an obstacle, this time a wire. Crawling along these obstacles to the left makes the path go all the way around the cell to get to the endpoint. Note that the extra loop made near the wire obstacle can be optimized away so that there are only seven turns rather than nine. The Hightower router is a variation of the maze technique that constructs paths from both ends until they intersect and complete a connection [Hightower].
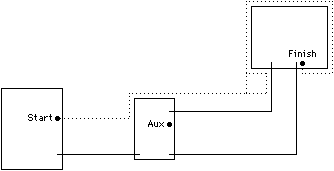 |
| FIGURE 4.9 Maze routing. |
The basic maze router is inadequate for many tasks, as the figure illustrates. For example, if the router chooses to walk to the right instead of to the left when it hits an obstacle, then it will quickly loop back to its starting point. This is an indication that it should change directions and start again. If the router then returns for the second time after walking both to the left and to the right, the wire cannot be routed. This is the case in Fig. 4.9 when an attempt is made to connect "start" to "aux." The only solution in such a situation is to change layers so that the wire can cross other wire obstacles.
Multilayer routing is an obvious extension to this basic technique. Typically the wire changes layers only long enough to bridge other wires that form an obstacle. Some schemes have one layer that runs horizontally and another layer that runs vertically [Doreau and Koziol; Kernighan, Schweikert, and Persky]. Routing on each layer is not difficult because all wires are parallel, so the only question is how to order sets of parallel paths. Since horizontal and vertical paths are already known, the location of layer contacts can be fixed so that the remaining problem is how to wire between them. This is done by swapping wires until they all fit through the available spaces and around the layer contacts. This scheme employs a constraint network that indicates how many wires can pass between any two obstacles. The network simplifies the computation of wire width and design-rule spacing. It ensures that wires will never form obstacles, but it creates a large number of layer contacts.
Other considerations must be addressed when doing multilayer routing. The most important is to minimize the number of layer changes. Contacts to other layers take up space on both layers and form obstacles for other wires. Also, excessive layer switching can delay a signal in the final circuit. Therefore the router should optimize the layer switches by refusing to make a change if it is not necessary for obstacle avoidance. A useful option to consider in multilayer routing is that there may be different starting and ending layers desired for a wire so that, once a layer change is made, the wire can remain in the layer to which it was switched. Of course, an alternative to switching layers is to route around the outside of an obstacle, which can consume much space. To allow for this without making absurd detours, some routers have parameters to choose between extra run length and extra layer changes for obstacle avoidance [Doreau and Koziol].
Another multilayer-routing consideration is the priority of layers. Since not all layers are the same, the speed of signals on a given layer should bias that layer's use. Also, some signals are restricted to certain layers. In IC layout, the power and ground wires must always run on metal layers [Keller]. When these wires cross other signals, it is the other signal that must change layers. One way to ensure this is to run the power and ground wires first; however, there must still be special code to ensure the correct placement of these wires. The PI system uses a traveling-salesman technique to find a path that runs through each cell only once in an optimal distance [Rivest]. Since this path never crosses itself, it divides the layout into two sides on which power and ground can be run without intersecting.
In printed-circuit routing, there are some signals that must run on specific layers. For example, those wires that are important in board testing must run on outside layers so that they can be probed easily. Therefore the multilayer router must allow special requests for certain wires' paths.
Routing an entire circuit one wire at a time can be difficult, because each wire is run without consideration for others that may subsequently be routed. Without this global consideration, total consistency is hard to achieve. Preordering of the wires to be routed can help in some circumstances. For example, if the wires are sorted by length and are placed starting with shortest, then the simple and direct wiring will get done without trouble and the longer wires will work around them. Alternatively, if the longest wires are run first, then they will be guaranteed to run and the short connections will have to struggle to complete the circuit. Another solution is to run wires in the most congested areas first [Doreau and Koziol]. This is a good choice because it most effectively avoids the problem of being unable to complete all the wiring.
Another option when routing many wires is the use of alternative routes for a wire. If each wire that is routed is kept on a stack, then this information can be used to back up when a new wire cannot be run. By backing up through the stack and undoing wires up to the offending wire that causes the blockage, an alternate path can be made so that subsequent wires can have a different environment that may be better (see Fig. 4.10). The nature of this routing change must be saved on the stack so that the same choice will not be made again if the router backtracks to that point a second time. If repeated backtracking to redo a wire exhausts the possibilities for that wire, backtracking must then go beyond the offending wire to an earlier one that allows even more possibilities. This process can be extremely time consuming as it repeatedly routes wires one at a time. With a little bookkeeping, much of the computing can be saved so that wires that reroute after a backtrack are routed faster. Nevertheless, there are no guarantees that recursive juggling of these wires will result in a good solution. One way to improve the chances for routing is to search the space of possible wire paths so that only those wires that promise no space increase are placed [Kernighan, Schweikert, and Persky].
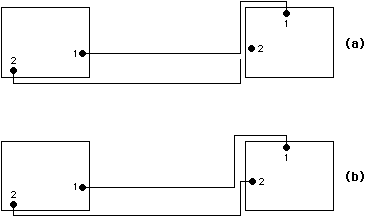 |
| FIGURE 4.10 Backtracking in routing: (a) First attempt to route net 2 (b) Backtracking reroutes net 1. |
Another way to manipulate single paths to obtain global consistency is with the simulated-annealing technique used in compaction [Kirkpatrick, Gelatt, and Vecchi; Sechen and Sangiovanni-Vincentelli]. Having a global measure of routing quality and making random changes allows each change to be seen either to help or to hinder the routing. Major changes, which are tried first, establish the overall routing configuration; minor changes are done last to get the details of the wiring correct. This method also consumes vast amounts of time, but achieves very good results.
| An alternative to single-wire routing is channel routing, in which all the wires in a channel are placed at once. This technique essentially sweeps through the routing area, extending all wires toward their final destination. Although this routing method can get stuck at the end of the channel and fail to complete many of the wires, it does make global considerations during the sweep so the results are often better than they are with maze routing. Also, it is faster because it considers all wires in parallel, examines the routing area only once, and avoids backtracking. Those routers that can handle connections on all sides of a routing area are called switchbox routers [Soukup] and they generally work the same way as channel routers. If the routing area is not rectangular, it must be broken into multiple rectangles and connection points assigned along the dividing lines (see Fig. 4.11). This step is called global routing or loose routing [Lauther]. |
|
Channel and switchbox routing typically make the assumption that wires run on a fixed-pitch grid, regardless of wire width or contact size. All contact points are also on these grid locations. Although this may consume extra space because of the need to use worst-case design rules, the area can always be compacted in a postprocessing step. Some routers are able to create new grid lines between the initial rows and columns if the new lines are necessary to complete the wiring successfully [Luk; Lauther].
Although there are many channel and switchbox routers [Deutsch; Rivest and Fiduccia; Doreau and Koziol], only one will be discussed; it combines good features from many others [Hamachi and Ousterhout]. This router works with a switchbox that contains connection points, obstacles, and obstructions and makes connections using two layers of wire (see Fig. 4.12). Obstructions are those areas that can be crossed only on certain layers. Obstacles block all layers, forcing the router to work around them.
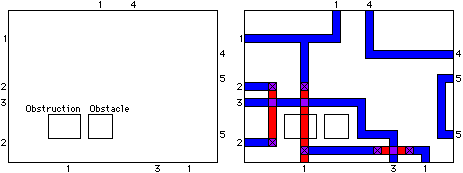 |
| FIGURE 4.12 Switchbox routing: (a) Initial configuration (b) After routing. |
The routing task is viewed as follows: Each net is in a particular horizontal track and must eventually get to a different horizontal track to complete its wiring. The wiring is run one column at a time, starting from the left and sweeping across the area. At each column, there are rules to determine which nets will switch tracks. When the sweep reaches the right side of the area, the layout is complete and all nets have been routed.
In order to implement this model for switchboxes, the nets connected at the top and bottom must be brought into the first horizontal track, and any connections to nets that are not on track centers must jog to the correct place. Once the nets are all on horizontal tracks, routing can begin.
As each column is processed, priority is given to those vertical wirings that can collapse a net. This is the case with the first column on the left in Fig. 4.12 that collapses net 2. Notice that the layer changes when running vertical wires. This allows vertical and horizontal tracks to cross without fear of connection. To prevent excessive layer switching, a postprocessing step eliminates unnecessary switches and moves contacts to maximize use of the preferred layer (if any).
The next priority in processing a column is to shift tracks toward a destination. Net 3 in the figure makes a downward jog as soon as it has cleared the obstacle so that it can approach its destination. Similarly, net 4 jogs down to its correct track immediately. Special rules must be used to handle the righthand side of the channel; otherwise wires like net 5 will not know their destination until it is too late. These rules reserve an appropriate number of columns to route the right edge.
In addition to these basic rules, there are much more complex ones that dictate when to create a contact, when to vacate a track in anticipation of an obstruction, and when to split a net in preparation for multiple end connections. When the rules are followed in the proper order, channel routing is achieved.
| In some situations the routing needs are specialized and can be solved more easily due to the problem's constraints. One such simplified technique is river routing, which connects many wires that are guaranteed not to cross, but instead run parallel to each other. River routing can be used to connect two cells that have incorrect pitch and alignment [Wardle et al.]. The issue in river routing is how to adjust the spacing properly if one end is wider than the other. One method runs the wires of the bus serially and constructs areas of avoidance after each wire [Tompa]. Figure 4.13 shows this process: The dotted lines are the areas of avoidance that are created after the wires are placed. Special methods such as this allow unusual routing needs all to be met in the wiring of a circuit. |
|
Placement, or floor-planning as it is sometimes called, is the process of positioning cells such that they connect well and do not waste space. Automatic placement tools therefore need to know the size of each cell and the complete set of routing requirements. Since this information is the same as what is required of routers, the two are often thought of as two parts of the same process. In fact, placement and routing comprise a single step in automatic printed-circuit-board layout. However, the two are often independent and have different algorithms driving them. Also, they must function separately as each produces results needed by the other: First, placement establishes an initial location of cells; next, routing connects the cells and indicates, by its success, how changes to the placement can help. The process is repeated until suitable layout is produced. Although an ideal placement and routing system would do these tasks uniformly, no such systems exist today. What is needed is to be able to share the placement and the routing goals in a common data structure so that the system can alternate between the two as the priorities change.
One system does approach this unification by dividing the overall placement and routing task into smaller pieces that are invoked alternately [Supowitz and Slutz]. This system observes that the vertical, lower channel of a T-shaped routing area needs to be routed before the horizontal, upper area. This T-shaped routing area is created by three cells on the left, right, and top. Routing the vertical, lower channel allows the cells on the left and right to be placed correctly. Then the upper area can be routed and the top cell can be placed correctly. The assumption is that a crude placement has already been done so that the placement and routing step can simply connect while fine-tuning the cell locations. Another assumption is that there is no cycle of T-shaped routing areas, which would prevent a good ordering of the placement and routing steps.
Automatic placement is difficult because of the extremely complex problems that it must satisfy. For example, if the wiring is ignored and only placement is considered, the task is simply one of tiling an area optimally, which is NP-complete [Garey and Johnson]. This means that the program for packing cells tightly can take an unreasonable amount of time to complete. If wiring considerations are added to this task, then every combination of cell placements that is proposed will also require seriously large amounts of time in routing. Because of these problems, placement cannot be done optimally; rather, it is done with heuristics that produce tolerably good results in small amounts of time.
One heuristic for automatic placement is min-cut [Breuer]. This technique divides the unplaced cells into two groups that belong on opposite sides of the chip. Each side is further subdivided until a tree-structured graph is formed that properly organizes all cells. Determination of the min-cut division is based on the wiring between the cells. The goal of min-cut is to make a division of cells that cuts the fewest wires (see Fig. 4.14). The number of cells should be divided approximately in two, such that each half has a high amount of internal connectivity and the two halves are minimally interconnected.
 |
| FIGURE 4.14 Min-cut placement method. The goal is to find a partitioning of the cells that results in the fewest wire cuts. |
The min-cut technique cannot do the whole job of placement. It considers neither cell sizes nor the relative orientation of cells within a group. However, it is one method of reducing the size of the problem by breaking it up into smaller subproblems. Another way of doing the same thing, called bottom-up [Rivest; Heller, Sorkin, and Maling], is conceptually the opposite of the min-cut method because it grows clusters rather than cutting them down.
| The bottom-up method of automatic placement presumes that all cells are distinct and must be grouped according to their needs. A weighting function is used to indicate how closely two cells match. This function, like the one for min-cut, counts the number of wires that can be eliminated by clustering two cells. It can also take cell sizes and other weights into account. Clustering then proceeds to group more and more cells until there is no savings to be had by further work. Figure 4.15 illustrates this technique. Initially, there are four unrelated cells. Bottom-up planning finds the two that fit together best by eliminating the most number of wires. In addition to considering wiring outside of cells, it is necessary to examine the complexity of wiring inside a cluster. If this were not done, then the optimal bottom-up clustering would be a single cluster with all cells and no external wires. |
|
Once min-cut or bottom-up methods have organized the cells into their relative orientations, a more precise placement is needed. This can be done by converting the placement graph into a dual graph that includes position [Kozminski and Kinnen]. The method recursively picks off edge members of the original graph and creates a new graph with position and size information. By proceeding in adjacency order, the new graph is built in a "brickwork" style.
An alternative to converting the placement graph into a more precise placement is to compute this information as the initial placement graph is built. In one system, the initial layout is seen as a square, and each min-cut division divides the square proportionally to the area of cells on each side of the cut [Lauther]. When min-cut is done, the square indicates proper area and position, but incorrect aspect ratio. The problem then is to fit the actual cells into the idealized areas of the square. A number of approximate methods are used, including rotating cells and spreading open the area. Since routing requirements may spread the layout further, this approximation is not damaging.
Besides min-cut and bottom-up methods, those that find analogies to physical systems that behave in similar ways also can be used to do placement. For example, if a circuit is viewed as a resistive network, in which each cell is a constant voltage node and each collection of intercell wires is a resistor, then the problem becomes one of finding the correct voltage. The voltage values that are close indicate cells that should be near. To implement this technique, the square of the wire lengths becomes the objective function that is solved with matrix techniques [Cheng and Kuh]. The resulting graph can then be adjusted into actual placement using the techniques already described.
Another physical emulation that is used for placement is simulated annealing [Kirkpatrick, Gelatt, and Vecchi; Sechen and Sangiovanni-Vincentelli]. This method was shown to be useful in compaction and routing, so it should be no surprise that it also works for placement. Given an initial floor-plan, the annealer makes severe changes and evaluates the results. The severity of the changes decreases until there is nothing but detail to adjust. Like the other annealing tasks, this method consumes large amounts of time but produces good results.
Other information can be used to produce more intelligent cell placement. For example, there can be special code to detect cells that align well and should be placed together. This can be done before the general-purpose placement begins. An idiomatic floor-planner is one that recognizes these special situations and uses appropriate algorithms in each case [Deas and Nixon]. Determining which idioms exist in the layout is done by examining the routing needs and applying specialized rules that recognize arrays, trees, complex switchboxes, and so on.
Once a basic placement has been found, it is possible to use other methods to fine-tune the layout. The results of routing will indicate the amount of channel utilization so that the cell spacing can be adjusted. This information can be used to control another iteration of placement or it can simply indicate the need for compaction of the final layout. It has also been shown that the placement and routing cycle can be shortened by having routing take place after every step of min-cut division [Burstein, Hong and Pelavin]. Once again, the results of routing help with subsequent placement.
Besides routing, other tools can be used to help improve the results of placement. One system even integrates timing information to help placement and routing iterations [Teig, Smith, and Seaton]. This timing analysis, described more fully in Chapter 5, finds the worst-case circuit delay so that the placed modules and routed wires can optimize that path.
Automatic placement is a difficult problem that has not yet been solved well. However, it is one of the few tasks in which hand design excels over machine design, so it is worth trying to solve. With good placement, automatic layout can become a useful reality. Until such time, these systems will provide alternative layouts from which a designer can choose.
The pads of an integrated-circuit chip are large areas of metal that are left unprotected by the overglass layer so they can be connected to the leads of the IC package. Although large compared to other circuit elements, the pads are very small and make a difficult surface on which to bond connecting wires. Automatic wire-bonding machines can make accurate connections, but they must be programmed for each pad configuration. The chip designer needs a tool that will help with all aspects of bonding pads.
The immediate objection of many designers to the offer of automatic pad layout is that they want to place the pads manually. Given that pads consume large areas, the designer often wants total placement control to prevent wasted space. Chips have not typically had many pads anyway, so manual techniques do not consume much time.
The answer to such objections is that any task, no matter how simple, must be automated in a complete design system. As the number of special-purpose chips increases and their production volume decreases, it will be more important to design automatically than to design with optimal space. Also, the programming of the bonding machine can become bottlenecked if it is not directly linked to the CAD system. In modern chips there can be hundreds of pads; placing them manually will lead to tedium and confusion. Finally, there are only a few considerations that must be kept in mind when doing pad layout and these can be easily automated.
One consideration in pad placement is that the pads should be near the perimeter of the chip. The bonding machine may spatter metal and do damage to the circuitry if it has to reach into the center. Some fabrication processes even require that no active circuitry be placed outside of the pads. Others, however, allow pads anywhere on the chip. Another reason to place pads on the edge is to keep the bonding wires from crossing. The pads must present an uncluttered view from the outside of the chip.
In addition to being located on the edge of the chip, pads should also be placed uniformly. This means that there must be approximately the same number of pads on all four edges and that they must be spaced evenly along each edge. On special chips that have rectangular layout, the pads may be evenly spaced along only two edges. Equal spacing makes automatic bonding easier, and uniform pad density keeps the bonding wires from cluttering and possibly shorting. The proper limitations of pad spacing must also be taken into consideration (currently no less than 200 microns between centers [Keller]).
One algorithm for pad placement is called roto-routing [Johannsen]. This technique starts by sorting the pads into the same circular sequence as are their connection points in the chip. The pads are then placed into a uniform spacing around the chip and rotated through all positions. The one position that minimizes overall wire length to the pads is used.
| Another concern in proper pad layout is the location of power and ground pads. Although some applications demand multiple power and ground pads for high power consumption, there are typically only one of each, and they should generally be on opposite sides of the chip, because they are usually bonded to leads that are on opposite sides of the package. In addition, they must be correctly connected to the other pads in order to get proper distribution of power and ground. Figure 4.16 shows one configuration of power, ground, and pads. The ground runs outside of the pads because it is less critical than the power rail, which runs just inside. This arrangement allows each pad to have easy access to the supply voltages it needs to function properly. In order to get these voltages to the chip, however, there must be a gap in the inner power rail. |
|
Routing of pad signals to the main chip circuitry can be done automatically with standard switchbox techniques. It is important to try to place the pads close to their destination so that signal wires do not run the length and width of the chip. Techniques for automatically assigning pads to signals can take into account both wire length and the importance of that signal's timing. For example, a two-phase clock brought in from outside should be placed on two pads that have similar distances to the active circuit.
Although bonding-pad placement is a minor aspect of integrated-circuit design, it is a necessary part of any good CAD system. Changing design methodologies call for tools that can do all the work and prevent minor oversights from turning into major failures. There are detailed constraints in pad layout, and failure to observe any one of them can cause the chip to fail totally.
| Previous | Table of Contents | Next | Static Free Software |